[양자역학 공부] (6) 유한 퍼텐셜 우물 문제 - 2

양자역학 독학 시리즈는 Coursera에서 볼 수 있는 콜로라도 볼더 대학교(University of Colorado, Boulder)의 박원장 교수님의 강의를 듣고 이해한 대로 정리한, 일종의 강의록 느낌입니다. https://www.coursera.org/learn/foundations-quantum-mechanics/

 

전 글에 이어서 이 문제를 마무리 할 예정입니다. 여태까지 중에 가장 간단한 글로 마무리해볼까 해요! 뒤에도 계속 문제들이 도사리고 있다는 점이 무섭네요.. 앞선 글을 안 보시면 전혀 이해가 안 가실 테니, 꼭 읽고 오셔야 해요!

[양자역학 공부] (5) 유한 퍼텐셜 우물 문제

 

 

목차

\(k,\;k_{0},\;E\)의 관계에 대한 기하학적 이해

회상을 해보자면, $$k=\sqrt{2mE\over\hbar^2},\;k_{0} = \sqrt{2m(V_{0}-E)\over\hbar^2}$$였습니다. 따라서 제목에서 밝힌 관계는 꽤나 밀접한데요! 이걸 기하학적으로 이해할 수 있다고 해요. 동일한 내용이 위키피디아에도 나오니 참고해도 좋겠어요! 

Finite potential well - Wikipedia

먼저 \(\eta = kL,\;\xi = k_{0}L\)라고 정의해봅시다. 그러면,

$$\begin{align} \eta^2 + \xi^2 &= (k^2 + k_{0}^2)L^2 \\ &= {{2m\left\{E +(V_{0}-E)\right\}L^2} \over \hbar^2 } \\ &= {{2mV_{0}L^2}\over\hbar^2}\end{align}$$

원의 방정식이네요! 눈에 보이시나요? 그리고, 앞선 글의 (7)(짝수 패리티), (10)(홀수 패리티)이 $$ \eta\tan(\eta) = \xi,\;\eta\cot(\eta) = -\xi$$가 됩니다.

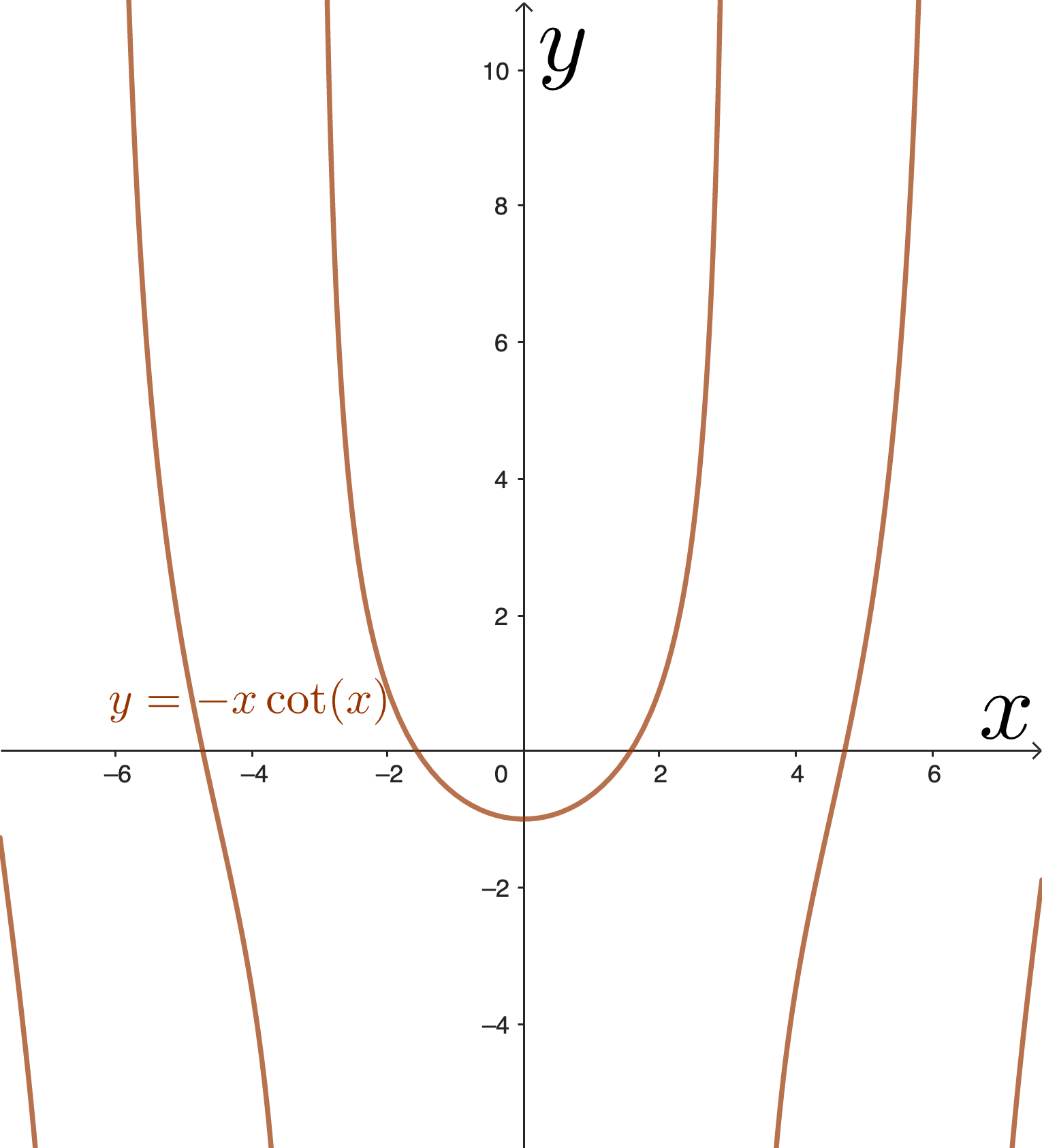이걸 원그래프와 같이 한번에 그래프로 그려보면 아래와 같이 된다고 해요. 아래에서의 \(y\)축이 \(\xi\), \(x\)축이 \(\eta\)가 되고, 조건 상 \(L\)도 \(k_{0},\;k\)도 양수여서 제1사분면만 보면 됩니다.

By Annafitzgerald - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=7600246

여기에서 빨간 선이 (7)에서 나오는 대칭적인 해(혹은 짝수 패리티), 노란 선이 (10)에서 나오는 반대칭적인 해(혹은 홀수 패리티)가 됩니다. 여기서는 빨간 선 2개와 노란 선 1개가 원과 교점을 가지네요. 순서대로 A, B, C라고 해봅시다.

놀라운 사실

여기서 먼저 짚고 넘어가야 하는 부분은,

• 원의 반지름: \( \sqrt{{2mV_{0}L^2}\over\hbar^2  }\)
• \(k=\sqrt{2mE\over\hbar^2}\)와 \(E\)는 비례관계, \(k_{0}= \sqrt{2m(V_{0}-E)\over\hbar^2}\)와 \(E\)는 반비례관계
• \(m,\;\hbar\;\)는 상수이므로 조절할 수 있는 것은 \(L,\;V_{0}\)입니다.
• 원의 반지름은 \(L,\;V_{0}\)가 커질 수록 커지고, 원과의 교점들 중 \(\eta = kL\)가 클 수록(쉽게 \(x\) 좌표 값이 클 수록) 에너지 \(E\)가 큰 상태입니다. 

그래서 알 수 있는 것은,

• 원의 크기는 우물벽의 높이가 높을 수록(퍼텐셜의 크기가 클 수록) 커집니다.
• 원과 빨간색 선의 교점(짝수 패리티) 혹은 노란색 선의 교점(홀수 패리티)만이 존재할 수 있는 경우의 수가 됩니다.
• 따라서, 가질 수 있는 \(\eta\) 값이 정해져 가질 수 있는 에너지 값이 정해집니다.
• 위의 그림의 경우에서, 주어진 원의 크기에 대해서 짝수 패리티 해 2개(A, C), 홀수 패리티 해 1개(B)를 가질 수 있는 셈입니다.
• A에서보다는 C에서 에너지 값이 더 높습니다. 제일 낮은 에너지를 갖는 홀수 패리티 상태는 A보다는 에너지가 크고 C보다는 작습니다.

그리고, 각 에너지 상태에 대해서 \(\psi(z)\)를 생각해서 그래프를 그려보면 다음과 같은 그림이 나옵니다. 위키피디아에 공개된 그림이어서 유도과정이 조금 다르므로, \(y\) 축에 \(E/V_{0}\)로 표시되어 있는데, 말 그대로 1.0이면 \(E=V_{0}\)이 되는 것입니다. 그리고 \(x\) 축의 숫자인 +5, -5는 각각 \(+L,\;-L\)으로 보시면 되겠습니다.

By Annafitzgerald - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=7600230

여기서 또 놀라운 점은, 우물 벽 안에서 \(\psi(z)\) 값이 0이 아니고, 그래서 입자가 존재할 확률이 0이 아니라는 것입니다. 무한 퍼텐셜 우물에서는 우물 벽 안에는 입자가 존재할 수 없다고 했고, \(\psi(z)\) 값이 0이었죠? 그래야 제곱인 확률이 0이 되니까요. 이외의 부분은 무한 퍼텐셜 우물 때와 비슷합니다.

• 우물 중심에 대칭이라는 점(우함수든 기함수든)도 동일하고, 
• 에너지가 양자화되어있다(quantized)는 점도 동일하고,
• 가장 낮은 에너지인 첫번째 짝수 패리티 해의 에너지 값이 0이 아니고,
• 여기서 역시 입자의 분포가 균일하지 않습니다.

다음 글에서는 조화 진동자(harmonic oscillator) 문제에 대해 다뤄보도록 하겠습니다.