양자역학 독학 시리즈는 Coursera에서 볼 수 있는 콜로라도 볼더 대학교(University of Colorado, Boulder)의 박원장 교수님의 강의를 듣고 이해한 대로 정리한, 일종의 강의록 느낌입니다. https://www.coursera.org/learn/foundations-quantum-mechanics/

이번엔 조화진동자 문제에 대해서 다뤄보도록 하겠습니다.
목차
고전역학의 조화진동자 문제
이런 용수철은 본 적 많으시죠? 이게 전형적인 조화진동자입니다. 조화진동자는 균형점을 기준으로 변위(displacement)가 생기면, 그 변위의 크기에 비례해서 되돌아가려는 힘인 복원력(restoring force)이 생기는 장치라고 보면 되겠습니다. 훅의 법칙(Hooke's law) 기억나시나요? 그 공식을 만족하는 스프링을 생각하시면 되는 거에요! 따라서 $$\vec{F} = -k\vec{x}$$를 만족합니다. \(k\)는 기억이 날 수도 있으려나요! 용수철상수에요. 벡터기호는 생략하고 뉴턴의 제2법칙을 적용하면, $$ma = m{d^2 x\over dt^2} = -kx$$가 되고, \(\omega = \sqrt{k\over m}\)으로 정의하면 $${d^2 x\over dt^2} = -\omega^2 x$$가 됩니다. 어디서 본 것 같죠?
[양자역학 공부] (3) 시간 비의존 슈뢰딩거 방정식
양자역학 독학 시리즈는 Coursera에서 볼 수 있는 콜로라도 볼더 대학교(University of Colorado, Boulder)의 박원장 교수님의 강의를 듣고 이해한 대로 정리한, 일종의 강의록 느낌입니다. https://www.coursera.o
sgsrvilla.tistory.com
시간-비의존 슈뢰딩거 방정식의 모양을 다시 보여드리면, $$-{\hbar^2 \over 2m} {\partial^2 \over \partial x^2} \psi(x) = E\psi(x)$$니까 $$\begin{align}{\partial^2 \psi(x) \over \partial x^2} &= - {2mE\over\hbar^2}\psi(x) \\ &= A\psi(x) \end{align}$$여서 이계도함수가 원함수의 상수배꼴이 되는, 위의 조화진동자와 유사한 형태를 가집니다. 이런 방정식의 해는 삼각함수꼴이었죠? 이런 걸 사인함수꼴(sinusoidal)이라고 합니다. 이런 삼각함수는 결국 각도와 연관이 있죠? 위에서 슬쩍 정의해둔 \(\omega\)가 각도와 관련이 있습니다. 주기운동을 보이는 조화진동자의 각진동수(angular frequency)라고 하는데요, 자세한 것은 일반물리학에 나올 건데, 당장 크게 중요하지 않으니 넘어가도록 할게요...

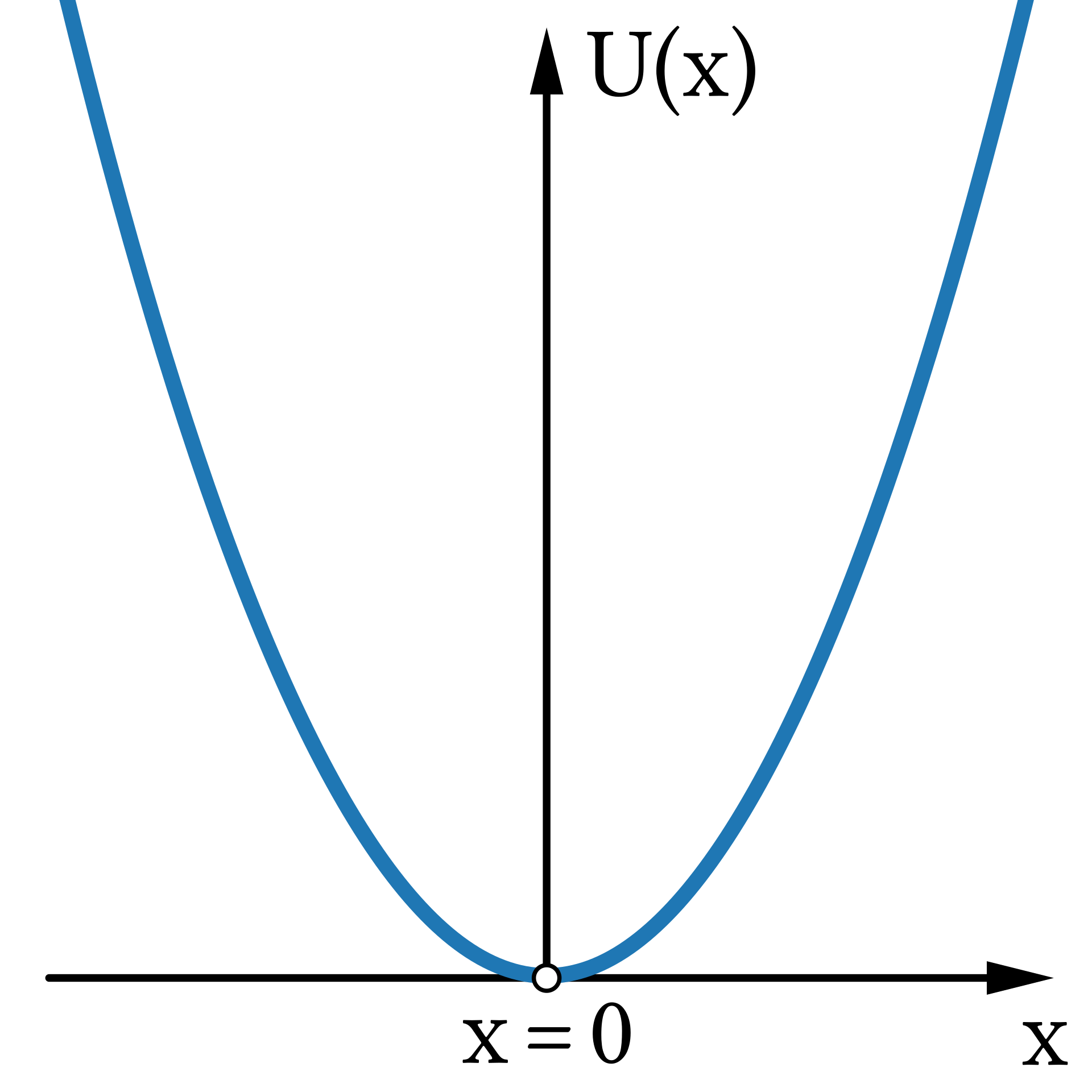
용수철의 퍼텐셜에너지(위치에너지)까지 기억이 나실 분은 거의 없으시겠죠? 어쨌든, 퍼텐셜에너지는 힘의 변위에 대한 적분과 관련된 것으로 생각하면 됩니다. 다음과 같이 정의로부터 계산할 수 있어요. $$\eqalign{V(x) &= -\int F(x)dx \\ &= -\int (-kx) dx \\ &= {1\over 2}kx^2 \\&= {1\over 2}m\omega^2 x^2}$$
양자조화진동자(Quantum harmonic oscillator)
풀어야 하는 방정식은?
이걸 해밀토니언(Hamiltoian) 내에 있는 퍼텐셜에너지 항에 대입해보면 되겠어요! 그러면 $$ \eqalign{\mathcal{H}\psi(x) &= \underbrace{\left[ -{\hbar^2\over 2m}{d^2 \over dx^2} + V(x) \right]}_{\rm {Hamiltonian \; operator}}\psi(x) \\ &= \left[ -{\hbar^2\over 2m}{d^2 \over dx^2} + {1\over 2}m\omega^2 x^2 \right] \psi(x) \\ &= E\psi(x)}$$ 여기서 \(\xi = \sqrt{m\omega \over \hbar} x\)로 정의하면, \(d\xi = \sqrt{m\omega \over \hbar}dx\)임을 이용하여 $$ {d^2 \psi \over d\xi^2} - \xi^2 \psi = -{2E\over \hbar\omega}\psi$$ 왜 도대체 이런 식으로 치환을 했을까 생각해보면, \(f^{\prime \prime}(x) - x^2 f(x) = C f(x)\) 형태를 만들면 깔끔하게 해가 나오는 공식 같은 것이 있어서 그런 것이 아닐까 싶지만, 별로 이유가 궁금하지는 않더라구요.
에르미트 다항식을 이용한 풀이
이전에는 푸리에 급수(Fourier series)를 이용하여 문제를 풀었었죠? 위의 방정식을 풀기 위해서 에르미트 다항식(Hermite polynomial)을 이용한다고 해요. 위키피디아를 찾아보니, 확률론자 버전, 물리학자 버전 등등 여러가지가 있는데, 여러 분야에서 사용되는 중요한 식인 것 같아요.
여기서 사용하는 에르미트 다항식은 다음과 같이 나타나요. $$H_{n} = (-1)^{n} e^{x^{2}} {d^n \over dx^n}(e^{-x^{2}})$$ 복잡하죠? 이걸 넣으면 미분방정식이 쉽게 풀리는 것일까요..? 어쨌든 저 미분방정식의 해를 $$\psi_{n}(\xi) = A_{n}H_{n}e^{-\xi^2 /2}$$의 형태로 구해보려고 한다고 해요. \(A_{n}\)는 \(n\)에 대해 나타나는 계수를 줄여서 표시한 거에요.
저 기괴하게 생긴 \(\psi_{n}\)을 위에서 얻은 방정식에 대입해보면, $$ {d^2 H(\xi) \over d\xi^2} -2\xi {d H(\xi) \over d\xi} +\left( {2E\over \hbar\omega}-1\right) = 0$$ 가 나옵니다. 이때 해가 존재하는 조건이 $$\eqalign{\left( {2E\over \hbar\omega}-1\right) &= 2n \\ E &= \left(n+{1\over 2} \right)\hbar\omega}$$라고 합니다. \(n\)은 0 이상의 정수입니다.
원래는 유도과정이 꽤나 길더라구요. 극한도 이용해야 하고... 처음부터 다 담으면 길어질 것 같으니 다른 글에서 따로 유도해보는 것으로 할게요. 이전 글에서는 길어도 다 유도했었지만, 여기서만큼은 결과 위주로 해볼게요!
정규화까지 고려하면 해를 얻습니다
$$\int_{-\infty}^{\infty}|\psi(x)|^2 dx = 1$$을 계산하면, $$A_{n} = \sqrt{1\over {\sqrt{\pi}2^n n!}}$$이 나온다고 해요. 이건 다른 글에서도 유도하지는 않겠습니다. 그리피스 책에서도 다른 책 보라는 식으로 되어 있어서 계산이 어렵지는 않은데 귀찮구나 하고 느꼈거든요.

이걸 다 대입하면 해를 얻습니다. $$ \psi_{n} (x) = \sqrt{{1\over {2^n n!}}{\sqrt{m\omega\over \hbar\pi}}}e^{-m\omega z^2 / 2\hbar} H_{n} \left( \sqrt{m\omega \over \hbar} z \right) $$
양자조화진동자의 특성

- 다시 에너지 식을 생각해보면, $$ E = \left(n+{1\over 2} \right)\hbar\omega,\;n=0,\;1,\;2,\;\dots$$ 그러니 제일 작은 에너지값은 \({\hbar\omega \over 2} \ne 0\)가 되어 또 이전의 내용들처럼 0이 아니게 됩니다. 이것은 양자역학에서만 나타나는 특이한 성질입니다.
- 추가적으로 특이한 것은, 에너지 준위의 간격이 일정하다는 것입니다. 그 간격은 \(\hbar\omega\)로 일정합니다. 위의 그림에도 잘 나타나 있습니다.
- 역시 대칭성(symmetry)과 반대칭성(anti-symmetry)를 가집니다. 패리티(parity) 내용 기억나시나요? \(n\)이 짝수면 중심선에 대칭인 우함수 형태의 짝수 패리티, 홀수면 중심점에 점대칭인 기함수 형태의 홀수 패리티가 나타납니다. 정규분포에서 잠시 나왔던 가우스함수(Gaussian function) 부분은 (\(e^{-x^{2}}\)) 항상 우함수이고, 상수 \(A_{n}\) 부분은 함수의 기우성을 정할 수 없으니 에르미트 다항식 부분이 파동함수의 기우성을 결정, 즉 대칭성을 결정하게 됩니다.
정상태(stationary state)에 대한 간단한 언급
추가적으로 수업에서는 정상태에 대해 언급되었습니다. 대단한 내용은 없으니 간단하게만 정리해보았어요.
- 시간-비의존 슈뢰딩거방정식으로 파동함수를 구했습니다. 실제 진동은 시간에 의존적이니까 실제 진동에 대한 뭔가를 구한 것은 아니네요. 우리가 구한 것은 멈춰있는 상태인 정상태에 대한 해를 구한 것입니다.
- 고전적인 조화진동자의 실제 진동에 대한 함수는 정상태에 대한 해를 구하고 그것들의 선형결합(linear combination) 형태로 나타낼 수 있었다고 합니다.
- 실제 진동자의 파동함수를 구하려면 시간-의존 슈뢰딩거 방정식을 풀어야 한다고 하네요.
다음 글에서는 퍼텐셜 계단(potential step)에 대해 다뤄보겠습니다. 디랙의 브라켓(bra-ket)까지 가는 것도 상당히 시간이 걸리네요. 그래도 조금씩 뭔가 배워나가는 느낌이긴 해서 좋지만 힘들기도 하네요...

'다른 공부들 > 물리' 카테고리의 다른 글
| [양자역학 공부] (9) 퍼텐셜 장벽 문제 (0) | 2023.09.02 |
|---|---|
| [양자역학 공부] (8) 퍼텐셜 계단 문제 (2) | 2023.08.31 |
| [양자역학 공부] (6) 유한 퍼텐셜 우물 문제 - 2 (0) | 2023.08.28 |
| [양자역학 공부] (5) 유한 퍼텐셜 우물 문제 (1) | 2023.08.28 |
| [양자역학 공부] (4) 고유치 문제와 힐베르트 공간의 구성 (0) | 2023.08.27 |




댓글